A Revolutionary Century in Logic: Boole to Gödel
Chris Goad, April 2023
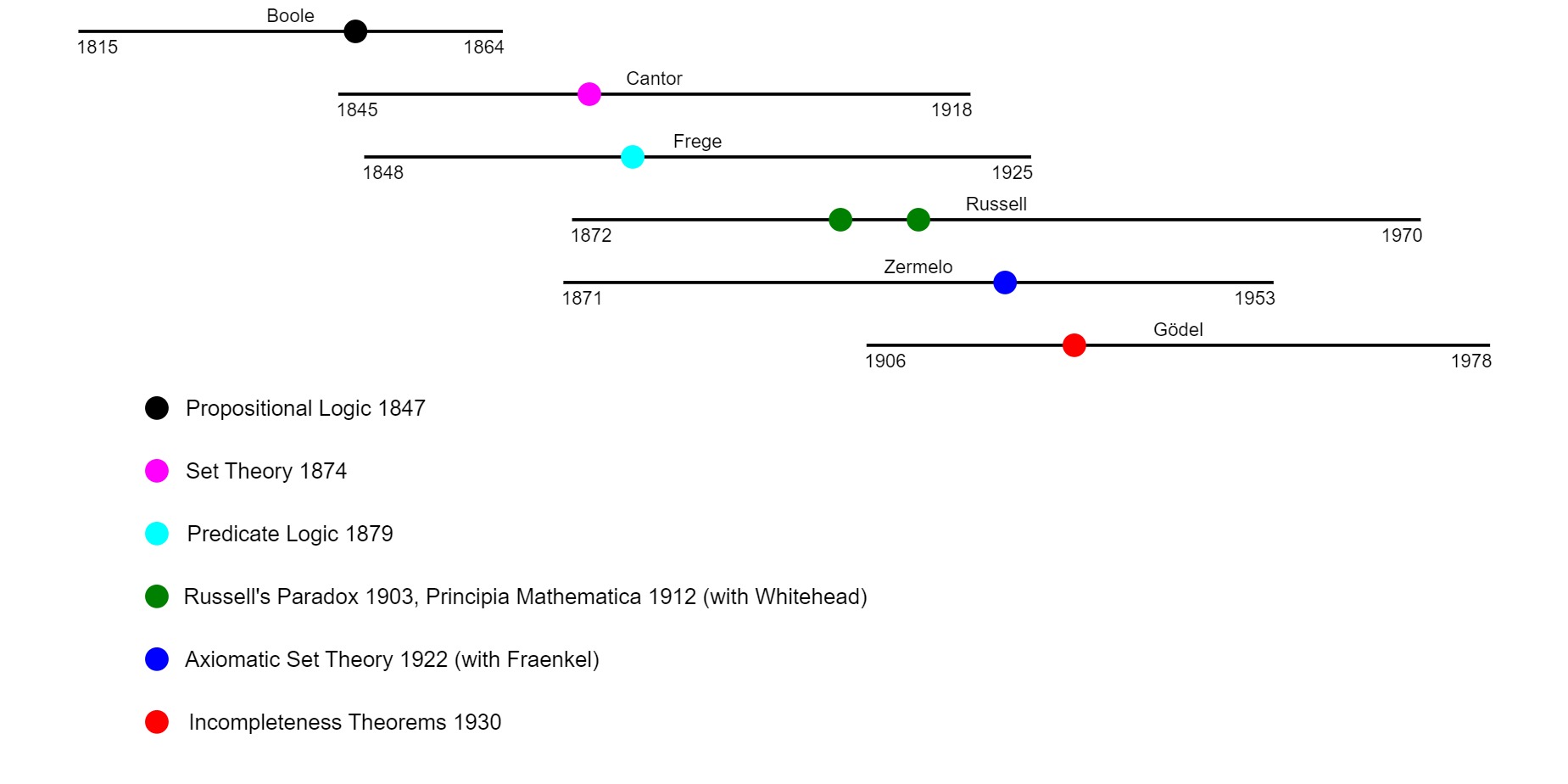
Now, to our topic: the developments in logic in Europe between the 1840s and the 1930s. These developments were primarily of a mathematical nature, in two senses. First, the kind of thought studied was often but not exclusively mathematical. Second, the logics invented during this period; propositional, predicate, and set theoretical, were formulated in mathematical terms.
First, a time line.

Boolean algebra, the system to which Boole's name is attached, resembles ordinary high school algebra except that the
variables take on the values 0 (for false) and 1 (for true), rather than real numbers, and that
the operators + (addition),* (multiplication),/ (division) and - (additive inverse), are replaced by the operators ∧(and), ∨(or), and ¬(not).
The tables for the boolean operators
are
0 ∧ 0 = 0, 0 ∧ 1 = 0, 1 ∧ 0 = 0, 1 ∧ 1 = 1
0 ∨ 0 = 0, 0 ∨ 1 = 1, 1 ∨ 0 = 1, 1 ∨ 1 = 1
¬0 = 1, ¬1 = 0
The useful notion that a implies b (written as a ⊃ b), can be defined as ¬a ∨ b.
A term constructed from the operators, such as a ∧ (b ∨ c) is called a proposition. A proposition is valid, if and only if, for all assignments of values 0 or 1 to the variabes, the value of the proposition is 1. For example a ∨ ¬a is valid as is ¬ (a ∧ ¬a). A valid proposition is also called a tautology.
It is possible to write down axioms (statements that are deemed true without proof) and rules of inference (rules for deriving the validity of a proposition from other propositions) via which every tautology can be proved. A proof is a sequence of steps, each of which derives its conclusion from axioms or propositions which have been derived earlier in the proof.
Then, just as theorems of ordinary algebra can be applied to actual numbers (think of the quadratic equation), so the theorems of Boolean algebra can be applied to actual propositions about the world. For example, suppose that our lawn in a tropical place becomes wet only via rain or sprinking . Consider the simple theorem of Boolean Algebra:
((a ⊃ (b ∨ c)) ∧ (¬b ∧ ¬c)) ⊃ ¬ a
then if a="wet grass", b="it sprinkled", and c="it rained", then since "wet grass"(a) does imply(⊃) "it sprinkled"(b) or(∨) "it rained"(c), we can conclude from our theorem that if it neither sprinkled nor rained, that our grass is not wet.
Boole himself did not formulate Boolean Algebra in its modern form, but he did invent the calculus of propositions upon which it is based
.A set is an unordered collection of elements. Bracket notation is conventionally used to denote sets. For example, the set of positive integers less than 5 could be written as {1,2,3,4}, or {1,4,3,2} (both denote the same set). Cantor was the first to investigate sets as mathematical objects. He considered infinite as well as finite sets. His most famous and most astounding discovery is that not all infinite sets are of the same size. Rather, there is an infinite hierarchy of infinite sets, each larger than the last.
By saying that sets A and B are of the same size, is meant that the members of the two sets can be placed into one-to-one correspondence. That is, size(A)= size(B) means that there is a set of pairs <a,b> where every element of A appears as the first element of some pair, every element of B appears as the second of some pair, and each element of A or B appears in exactly one pair. Under this definition of size (called cardinality), the cardinality of the positive integers is the same as the cardinality of the even positive integers. A set of pairs which proves this is <1,2>,<2,4><3,6> ... <n,2*n> ....
Cantor's proof that there is at least one set of cardinality greater than that of the integers is as follows. Consider the set of all infinite sequences of 0s and 1s. Suppose there is some way of pairing these sequences up with the positive integers (which has the same cardinality as the set of all integers). Let the sequence paired with the integer n be named Sn. Then we could write something like
s1: 0 1 0 1 1 1 ...
s2: 1 0 1 1 1 1 ...
s3: 0 1 1 1 0 0 ...
.
.
.
Consider the sequence D constructed by running down the diagonal, and reversing each value. For our little example, D would start 1 1 0. D then differs from every sequence in our pairing at one point. Therefore, D is not in the pairing, contrary to the assumption that every sequence appears there. There are more binary sequences than integers. The set of the integers, and all other sets of the same cardinality, are called "countable". All other infinite sets are called called "uncountable".
Cantor showed, with a similarly simple proof, that for every infinite set, there is a bigger one.
Why is set theory such a big deal? Answer: it was realized, in the late 19th century, that essentially all of mathematics is present within set theory. That is, all of the structures that mathematicians study, from various kinds of numbers (integers, rationals, reals, complex, quaternions), geometric structures of all dimensions, algebraic structures such as groups, rings, and fields, and things far more exotic, can all be represented as sets of one kind or another, and all of the reasoning about them can be cast as reasoning about sets.
Frege contributed in many ways to the development of logic, but the contribution which had the most long-term impact was his predicate logic, introduced in his Begriffsschrift, published in 1879. Its elementary terms are assertions that a given relation R holds for certain values, written in the form R(x,y,z...). Predicate logic is applicable to many mathematical domains, and each defines its own set of relations. One is Peano arithmetic, where the fundamental relations are S(a,b) (the successor relation), meaning that a+1 = b, and E(a,b) meaning that a and b are equal. Set theory (see Zermelo) and the theory of groups provide other examples. Given a particular domain, complex propositions are constructed using ∀ (for all) and ∃ (there exists), as well as the boolean operators ∧, ∨, and ¬. For example, the proposition ∀ (x) (∃ (y) S(x,y)) means that for all values of x, there exists a y which is the successor of x. As with boolean logic, several systems of proof have been defined. Charles Sanders Pierce formulated this variety of logic independently.
At the start of the 20th century, Russell and Frege, among others, were attempting axiomatization of set theory. Arithmetic had already been axiomatized in several ways by Peano (1889) and others. In any case, Russell identified a problem in Frege's approach, called Russell's paradox. Using Frege's axioms one could define the following set: the set of all sets that do not contain themselves. Call this set R. Does R contain itself? If it does, then by definition it does not. If it does contain itself, by definition it also cannot. Contradiction! Frege was not able to overcome this contradiction.
Principia Mathematica, a book in three volumes by Russell and his colaborator Whitehead, axiomatized set theory in a way that dodged Russell's paradox. Other mathematical domaims were axiomatized as well, independent of set theory. The book was an important effort. However, its formalisms were lengthy and complex, and it was critized by Gödel among others for inexactness of formalism. In any case the Zermelo-Fraenkel axioms came along a decade later, and mathematicians have used that formalism since.
Zermelo and Fraenkel's axioms for set theory were published in 1922. They consist of 12 axioms and axiom schemas (in which there are variables that range over terms, rather than sets), and they are expressed in Frege's predicate calculus. A line or two of text suffices to write each down. After a century of use, no contradiction has been found. This is remarkable! In a page or two one can write down a foundation for essentially all of mathematics.
There are several proof systems for predicate logic (notably, the sequent calculus, the tableau method, and "natural deduction"). Each can be used to build proofs of set theoretic propositions using the Zermelo-Fraenkel axioms. And in each system, a fully formalized proof, which follows the rules of deduction in the system exactly, can be checked mechanically - i.e. by computer. Computer programs for checking proofs have been around since the 1960s, as have proof assistants which allow interactive construction of fully formal proofs by mathematicians. Not all proofs have been fully formalized, far from it. A convincing informal proof differs from a formal proof in that some details are stepped over, but in a manner that conforms to what the mathematical community judges to retain the validity of the proof. The common conviction, against which no evidence has been seen in a century, is that such details can always be filled in if needed.
With Zermelo-Fraenkel set theory in place, with its (equivalent) mechanical systems of proof, it became natural to wonder whether the systems of proof are complete - whether every true statement is provable in the systems.
The young Gödel proved otherwise. He showed that in any consistent (non-self-contradictory) system which includes arithmetic, that there are true statements that cannot be proved within the system. In a way this was as radical as the development of set theory itself. For a decade it seemed that virtually the whole of mathematics could be captured by a formal system. But no, the capture must always be partial. Mathematical truth can never be captured by any formal system, not even arithmetic truth.
Gödel 's method was as follows. First he showed how to assign a number to each statement of arithmetic, called its Gödel number. Then he showed how the notion of a formally provable statement could be defined by an arithmetic expression. Call it P. So, P(x) means that x is the Gödel number of a provable statement. Then he showed how to construct a statement meaning roughly ¬P(this statement's own Gödel number). In other words, "I am not provable". If this statement is true, then we have our true but unprovable statement. If it is false, ie it is provable, we have a contradiction, contrary to assumption.
This is Gödel's first incompleteness theorem. The second states that no formal system which contains arithmetic can prove its own consistency.